Intuitivamente imaginamos un hilo delgado y estirado , consideramos dos puntos donde cortamos el hilo: la pieza que obtenemos es la imagen de un intervalo finito, los puntos de corte pueden o no estar en la pieza. En el caso de tomar solo un punto y cortar, cualquiera de las piezas separadas es la imagen de un intervalo infinito, lo mismo que todo el hilo.

A los números que aparecen en el intervalo se les llama extremos del intervalo.
Si el extremo del intervalo no se incluye, el corchete se escribe al revés : “]” al principio y “[” al final.
El símbolo “∞” representa el infinito, mientras que “–∞” representa menos infinito. Estos símbolos en un
intervalo indican que no existe otro número que sea extremo del intervalo.
El corchete correspondiente a –∞ o ∞ se coloca al revés, por ejemplo: “]–∞, 8]” y “]1, ∞[”.

En la notación de conjunto, por ejemplo, el conjunto {x ∈ ℝ | a ≤ x ≤ b} se lee: los elementos x que pertenecen a los números reales tal que x es mayor o igual que a y menor o igual que b.


Unión de intervalos
La unión de dos intervalos A y B es el conjunto de todos los números que están en el intervalo A o bien están en el intervalo B o bien están en los dos intervalos a la vez.
Se representa con el símbolo ∪. Por ejemplo, la unión de dos intervalos se puede representar así:


Vamos a ver ahora cómo calcular la unión de dos intervalos al mimos tiempo que resolvemos unos ejemplos.
Empezamos por el primero:

En primer lugar, representamos el primer intervalo (-5,0] en la recta numérica. El primer intervalo comienza en -5, abierto por la izquierda, luego se representa un punto vacío y termina en 0, cerrado por la derecha, por lo que se representa con un punto lleno:

Ahora, en la misma recta, representamos el segundo intervalo (-1,∞), que comienza en -1 con un punto vacío ya que está abierto por la izquierda y termina es infinito, que siempre es un intervalo abierto y por tanto no se incluye en el intervalo:

La unión de estos dos intervalos corresponde con la parte de la recta que se queda coloreada, bien del primer intervalo (rojo), bien del segundo intervalo (azul) o por los dos intervalos (rojo y azul).
La parte coloreada de algún color empieza en -5 con un punto vacío, por lo que será abierto por la izquierda y termina en infinito, que al ser infinito queda abierto por la derecha:
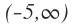
Nota: Date cuenta que el -1, está vacío por el segundo intervalo, pero queda relleno por el primer intervalo, y por tanto pertenece a la unión.
Vamos a ver otro ejemplo de unión de intervalos:

Representamos el primer intervalo [-1,3) en la recta numérica: Está cerrado por la derecha, por lo que ponemos un punto lleno en -1 y abierto por la izquierda, por lo que en -3 corresponde un punto vacío:

Representamos el segundo intervalo (2,4) en la misma recta. Es un intervalo abierto, por lo que empieza en 2 con un punto vacío y termina en 4 con otro punto vacío:

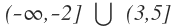


La intersección de intervalos es la parte común a los dos intervalos. En este caso, la parte común empieza en 1 y termina en 2.
El 1 está relleno por el primer intervalo, pero hay un punto vacío por el segundo intervalo, luego no es común a los dos y por tanto se queda abierto por la izquierda.
El 2 tiene un punto vacío por el primer intervalo y se queda relleno por el segundo intervalo. Como tampoco es común a los dos intervalos, queda abierto por la derecha.
La intersección de ambos intervalos nos queda entonces:
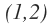
Vamos a ver cómo calcular la intersección de dos intervalos cuando estos se encuentran separados en la recta real.
Por ejemplo:

Representamos ambos intervalos en la recta real y nos queda:

En este caso, los intervalos no tienen ningún punto en común, luego la intersección de intervalos sería el conjunto vacío:

Simbólicamente: A - B = {x Î R / x Î A Ù x Ï B}
Se representa con el símbolo ∪. Por ejemplo, la unión de dos intervalos se puede representar así:


Vamos a ver ahora cómo calcular la unión de dos intervalos al mimos tiempo que resolvemos unos ejemplos.
Empezamos por el primero:

En primer lugar, representamos el primer intervalo (-5,0] en la recta numérica. El primer intervalo comienza en -5, abierto por la izquierda, luego se representa un punto vacío y termina en 0, cerrado por la derecha, por lo que se representa con un punto lleno:

Ahora, en la misma recta, representamos el segundo intervalo (-1,∞), que comienza en -1 con un punto vacío ya que está abierto por la izquierda y termina es infinito, que siempre es un intervalo abierto y por tanto no se incluye en el intervalo:

La unión de estos dos intervalos corresponde con la parte de la recta que se queda coloreada, bien del primer intervalo (rojo), bien del segundo intervalo (azul) o por los dos intervalos (rojo y azul).
La parte coloreada de algún color empieza en -5 con un punto vacío, por lo que será abierto por la izquierda y termina en infinito, que al ser infinito queda abierto por la derecha:
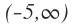
Nota: Date cuenta que el -1, está vacío por el segundo intervalo, pero queda relleno por el primer intervalo, y por tanto pertenece a la unión.
Vamos a ver otro ejemplo de unión de intervalos:

Representamos el primer intervalo [-1,3) en la recta numérica: Está cerrado por la derecha, por lo que ponemos un punto lleno en -1 y abierto por la izquierda, por lo que en -3 corresponde un punto vacío:

Representamos el segundo intervalo (2,4) en la misma recta. Es un intervalo abierto, por lo que empieza en 2 con un punto vacío y termina en 4 con otro punto vacío:

La unión de los dos intervalos es la parte de la recta que se queda coloreada de algún color (o de ambos). En este caso empieza en -1 con un punto lleno y termina en 4 con un punto vacío, por tanto, el intervalo será cerrado por la izquierda y abierto por la derecha:
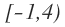
Hay casos donde los intervalos están separados en la recta real, como por ejemplo el siguiente:
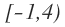
Hay casos donde los intervalos están separados en la recta real, como por ejemplo el siguiente:
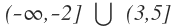
Si representamos ambos intervalos en la recta numérica nos queda:
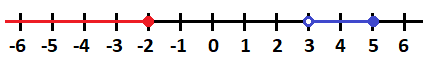
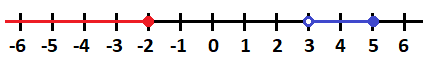
En este caso, la unión de intervalos no puede expresarse en un sólo intervalo, por lo que sigue siendo la unión de dos intervalos y no puede expresarse de otra forma:
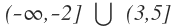
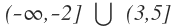
Intersección de intervalos
La intersección de dos intervalos A y B es el conjunto de todos los números que es común en el intervalo A y en el intervalo B.
Se representa con el símbolo ∩. Por ejemplo, la intersección de dos intervalos se puede representar así:


Se representa con el símbolo ∩. Por ejemplo, la intersección de dos intervalos se puede representar así:


Para calcular la intersección de dos intervalos, primero representamos ambos en la misma recta numérica y una vez representados, la intersección de intervalos corresponderá con la parte de la recta en la que coinciden los dos intervalos.
Por ejemplo, vamos a calcular la intersección de los siguientes intervalos:

Por ejemplo, vamos a calcular la intersección de los siguientes intervalos:

Representamos el primer intervalo (-4,3] en la recta, que comienza en -4 con un punto vacío y termina en 3 con un punto lleno, ya que está abierto por la izquierda y cerrado por al derecha:
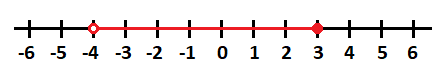
En la misma recta representamos el segundo intervalo (0,2], que comienza en 0 con un punto vacío y termina en 2 con un punto lleno, al estar abierto por la izquierda y cerrado por al derecha:
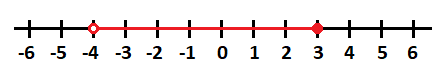
En la misma recta representamos el segundo intervalo (0,2], que comienza en 0 con un punto vacío y termina en 2 con un punto lleno, al estar abierto por la izquierda y cerrado por al derecha:

La parte donde coinciden ambos intervalos, es decir, que primero hemos pintado de rojo y después de azul, será la intersección de los intervalos. Es decir, es la parte donde coinciden los dos colores.
En nuestro caso, el tramo donde coinciden los dos intervalos empieza en 0 y termina en 2. El 0 está coloreado por el primer intervalo, pero tiene un punto vacío por el segundo intervalo, luego no es común a los dos intervalos y por tanto se queda fuera de la intersección, por lo que lo dejamos abierto por la izquierda.
El 2 está coloreado por el primer intervalo y tiene un punto lleno por el segundo intervalo, luego es común a ambos intervalos y por tanto, lo incluimos en la intersección cerrándolo con un corchete por la derecha.
Por tanto, la intersección de intervalos es:
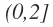
En nuestro caso, el tramo donde coinciden los dos intervalos empieza en 0 y termina en 2. El 0 está coloreado por el primer intervalo, pero tiene un punto vacío por el segundo intervalo, luego no es común a los dos intervalos y por tanto se queda fuera de la intersección, por lo que lo dejamos abierto por la izquierda.
El 2 está coloreado por el primer intervalo y tiene un punto lleno por el segundo intervalo, luego es común a ambos intervalos y por tanto, lo incluimos en la intersección cerrándolo con un corchete por la derecha.
Por tanto, la intersección de intervalos es:
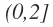
Vamos a ver otro ejemplo:


Representamos el primer intervalo [-2,2), que empieza en -2 con un punto lleno y termina en 2 con un punto vacío, al ser un intervalo cerrado por la derecha y abierto por la izquierda:

En la misma recta numérica representamos el segundo intervalo (1,4) que empieza en -1 con un punto vacío y termina en 4 con otro punto vacío, al ser un intervalo abierto:


La intersección de intervalos es la parte común a los dos intervalos. En este caso, la parte común empieza en 1 y termina en 2.
El 1 está relleno por el primer intervalo, pero hay un punto vacío por el segundo intervalo, luego no es común a los dos y por tanto se queda abierto por la izquierda.
El 2 tiene un punto vacío por el primer intervalo y se queda relleno por el segundo intervalo. Como tampoco es común a los dos intervalos, queda abierto por la derecha.
La intersección de ambos intervalos nos queda entonces:
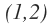
Vamos a ver cómo calcular la intersección de dos intervalos cuando estos se encuentran separados en la recta real.
Por ejemplo:

Representamos ambos intervalos en la recta real y nos queda:

En este caso, los intervalos no tienen ningún punto en común, luego la intersección de intervalos sería el conjunto vacío:

Diferencia de intervalos
Dados los conjuntos A y B, la diferencia, son sólo los elementos del conjunto A.Simbólicamente: A - B = {x Î R / x Î A Ù x Ï B}
Ejemplo:


